Einführung in LLMs-Texteinbettungen für SEO mit Beispielen

Wenn Sie SEO-Experte oder Digital-Marketer sind und diesen Artikel lesen, haben Sie in Ihrer täglichen Arbeit möglicherweise bereits mit KI und Chatbots experimentiert.
Die Frage ist jedoch: Wie können Sie KI optimal nutzen, ohne eine Chatbot-Benutzeroberfläche zu verwenden?
Dafür benötigen Sie ein tiefgreifendes Verständnis der Funktionsweise großer Sprachmodelle (LLMs) und müssen die Grundlagen des Programmierens beherrschen. Und ja, Programmieren ist heutzutage absolut notwendig, um als SEO-Profi erfolgreich zu sein.
Dies ist der erste einer Reihe von Artikeln, die darauf abzielen, Ihre Fähigkeiten zu verbessern, damit Sie LLMs verwenden können, um Ihre SEO-Aufgaben zu skalieren. Wir glauben, dass diese Fähigkeit in Zukunft für den Erfolg erforderlich sein wird.
Wir müssen mit den Grundlagen beginnen. Sie enthalten wichtige Informationen, sodass Sie später in dieser Reihe LLMs verwenden können, um Ihre SEO- oder Marketingbemühungen für die mühsamsten Aufgaben zu skalieren.
Im Gegensatz zu anderen ähnlichen Artikeln, die Sie gelesen haben, beginnen wir hier am Ende. Das folgende Video zeigt, was Sie tun können, nachdem Sie alle Artikel der Serie zur Verwendung von LLMs für SEO gelesen haben.
Unser Team verwendet dieses Tool, um die interne Verlinkung zu beschleunigen und gleichzeitig die menschliche Aufsicht aufrechtzuerhalten.
Hat es Ihnen gefallen? Das können Sie schon bald selbst bauen.
Beginnen wir nun mit den Grundlagen und vermitteln Ihnen das erforderliche Hintergrundwissen zum Thema LLM.
Was sind Vektoren?
In der Mathematik sind Vektoren Objekte, die durch eine geordnete Liste von Zahlen (Komponenten) beschrieben werden, die den Koordinaten im Vektorraum entsprechen.
Ein einfaches Beispiel für einen Vektor ist ein Vektor im zweidimensionalen Raum, der durch (x,y) dargestellt wird. Koordinaten wie unten dargestellt.
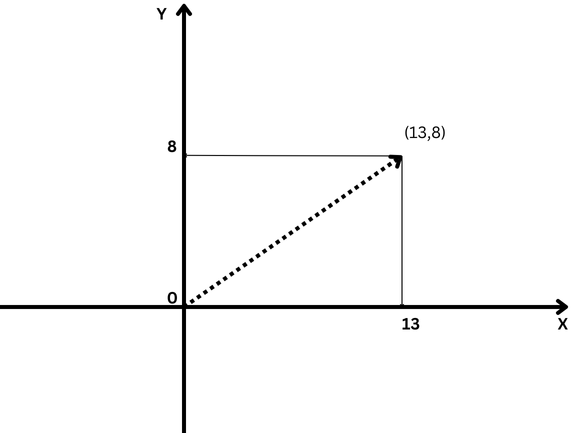 Beispiel eines zweidimensionalen Vektors mit den Koordinaten x=13 und y=8 in der Notation (13,8)
Beispiel eines zweidimensionalen Vektors mit den Koordinaten x=13 und y=8 in der Notation (13,8)In diesem Fall stellt die Koordinate x=13 die Länge der Vektorprojektion auf der X-Achse dar und y=8 die Länge der Vektorprojektion auf der Y-Achse.
Vektoren, die mit Koordinaten definiert sind, haben eine Länge, die als Vektorgröße oder Norm bezeichnet wird. Für unseren zweidimensionalen vereinfachten Fall wird sie mit der Formel berechnet:
Die Mathematiker gingen jedoch noch einen Schritt weiter und definierten Vektoren mit einer beliebigen Anzahl abstrakter Koordinaten (X1, X2, X3 … Xn), die als „N-dimensionaler“ Vektor bezeichnet werden.
Bei einem Vektor im dreidimensionalen Raum wären das drei Zahlen (x,y,z), die wir noch interpretieren und verstehen können, aber alles darüber liegt außerhalb unserer Vorstellungskraft und alles wird zu einem abstrakten Konzept.
Und hier kommen LLM-Einbettungen ins Spiel.
Was ist Texteinbettung?
Texteinbettungen sind eine Teilmenge von LLM-Einbettungen, bei denen es sich um abstrakte hochdimensionale Vektoren handelt, die Text darstellen und semantische Kontexte und Beziehungen zwischen Wörtern erfassen.
Im LLM-Jargon werden „Wörter“ als Datentoken bezeichnet, wobei jedes Wort ein Token ist. Abstrakter ausgedrückt sind Einbettungen numerische Darstellungen dieser Token, die Beziehungen zwischen beliebigen Datentoken (Dateneinheiten) kodieren, wobei ein Datentoken ein Bild, eine Tonaufnahme, ein Text oder ein Videobild sein kann.
Um zu berechnen, wie ähnlich Wörter semantisch sind, müssen wir sie in Zahlen umwandeln. So wie man Zahlen subtrahiert (z. B. 10-6=4) und erkennt, dass der Abstand zwischen 10 und 6 4 Punkte beträgt, ist es möglich, Vektoren zu subtrahieren und zu berechnen, wie ähnlich die beiden Vektoren sind.
Daher ist das Verständnis von Vektordistanzen wichtig, um zu begreifen, wie LLMs funktionieren.
Es gibt verschiedene Möglichkeiten, den Abstand zwischen Vektoren zu messen:
- Euklidische Entfernung.
- Kosinusähnlichkeit oder -distanz.
- Jaccard-Ähnlichkeit.
- Entfernung von Manhattan.
Jeder hat seine eigenen Anwendungsfälle, wir werden jedoch nur häufig verwendete Kosinus- und euklidische Distanzen besprechen.
Was ist die Kosinus-Ähnlichkeit?
Es misst den Kosinus des Winkels zwischen zwei Vektoren, d.h. wie eng diese beiden Vektoren beieinander liegen.
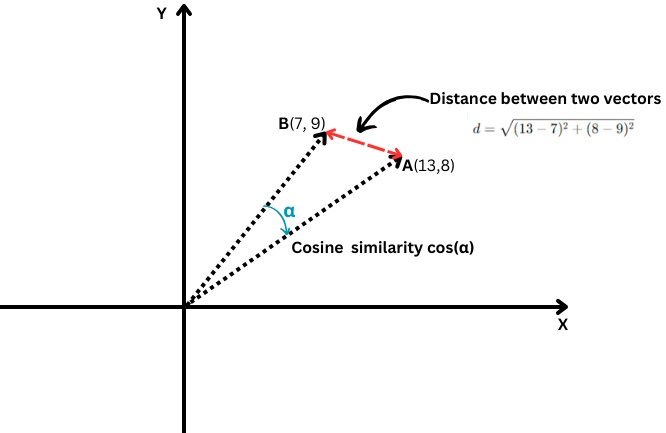 Euklidische Distanz vs. Kosinus-Ähnlichkeit
Euklidische Distanz vs. Kosinus-ÄhnlichkeitEs wird wie folgt definiert:
Dabei wird das Skalarprodukt zweier Vektoren durch das Produkt ihrer Beträge bzw. Längen geteilt.
Die Werte reichen von -1 (völlig entgegengesetzt) bis 1 (identisch). Der Wert „0“ bedeutet, dass die Vektoren senkrecht zueinander stehen.
In Bezug auf Texteinbettungen ist das Erreichen eines exakten Kosinus-Ähnlichkeitswerts von -1 unwahrscheinlich, aber hier sind Beispiele für Texte mit 0 oder 1 Kosinus-Ähnlichkeiten.
Kosinus-Ähnlichkeit = 1 (identisch)
- „Top 10 Geheimtipps für Alleinreisende in San Francisco“
- „Top 10 Geheimtipps für Alleinreisende in San Francisco“
Diese Texte sind identisch, daher wären ihre Einbettungen gleich, was zu einer Kosinus-Ähnlichkeit von 1 führt.
Kosinus-Ähnlichkeit = 0 (senkrecht, was bedeutet, nicht verwandt)
- “Quantenmechanik”
- „Ich liebe regnerische Tage“
Diese Texte haben keinerlei Bezug zueinander, was zu einer Kosinus-Ähnlichkeit von 0 zwischen ihren BERT-Einbettungen führt.
Wenn Sie jedoch das Einbettungsmodell „text-embedding-preview-0409“ von Google Vertex AI ausführen, erhalten Sie 0,3. Mit den Modellen „text-embedding-3-large“ von OpenAi erhalten Sie 0,017.
(Hinweis: In den nächsten Kapiteln lernen wir ausführlich, wie man Einbettungen mit Python und Jupyter übt.)
Wir überspringen den Fall mit Kosinus-Ähnlichkeit = -1, da dies höchst unwahrscheinlich ist.
Wenn Sie versuchen, eine Kosinus-Ähnlichkeit für Text mit gegensätzlichen Bedeutungen wie „Liebe“ vs. „Hass“ oder „das erfolgreiche Projekt“ vs. „das scheiternde Projekt“ zu ermitteln, erhalten Sie mit dem Modell „text-embedding-preview-0409“ von Google Vertex AI eine Kosinus-Ähnlichkeit von 0,5 bis 0,6.
Dies liegt daran, dass die Wörter „Liebe“ und „Hass“ häufig in ähnlichen Kontexten mit Bezug zu Emotionen vorkommen und „erfolgreich“ und „scheitern“ beide mit Projektergebnissen in Zusammenhang stehen. Die Kontexte, in denen sie verwendet werden, können sich in den Trainingsdaten erheblich überschneiden.
Die Kosinus-Ähnlichkeit kann für die folgenden SEO-Aufgaben verwendet werden:
- Einstufung.
- Stichwort-Clusterbildung.
- Weiterleitungen implementieren.
- Interne Verlinkung.
- Erkennung doppelter Inhalte.
- Inhaltsempfehlung.
- Wettbewerbsanalyse.
Bei der Kosinusähnlichkeit liegt der Schwerpunkt auf der Richtung der Vektoren (dem Winkel zwischen ihnen) und nicht auf ihrer Größe (Länge). Dadurch kann sie semantische Ähnlichkeiten erfassen und bestimmen, wie eng zwei Inhaltsteile übereinstimmen, selbst wenn einer viel länger ist oder mehr Wörter verwendet als der andere.
Ziel der nächsten Artikel, die wir veröffentlichen, wird es sein, tiefer in jeden dieser Bereiche einzutauchen und ihn zu erkunden.
Was ist die euklidische Distanz?
Falls Sie zwei Vektoren A(X1,Y1) und B(X2,Y2) haben, wird die euklidische Distanz mit der folgenden Formel berechnet:
Es ist, als würden Sie mit einem Lineal die Entfernung zwischen zwei Punkten messen (die rote Linie im Diagramm oben).
Die euklidische Distanz kann für die folgenden SEO-Aufgaben verwendet werden:
- Auswerten der Keyword-Dichte im Inhalt.
- Auffinden von doppelten Inhalten mit ähnlicher Struktur.
- Analysieren der Ankertextverteilung.
- Stichwort-Clusterbildung.
Hier ist ein Beispiel für die Berechnung der euklidischen Distanz mit einem Wert von 0,08 (nahezu 0) für doppelten Inhalt, bei dem die Absätze einfach vertauscht sind. Das bedeutet, dass die Distanz 0 beträgt, d. h. der Inhalt, den wir vergleichen, ist derselbe.
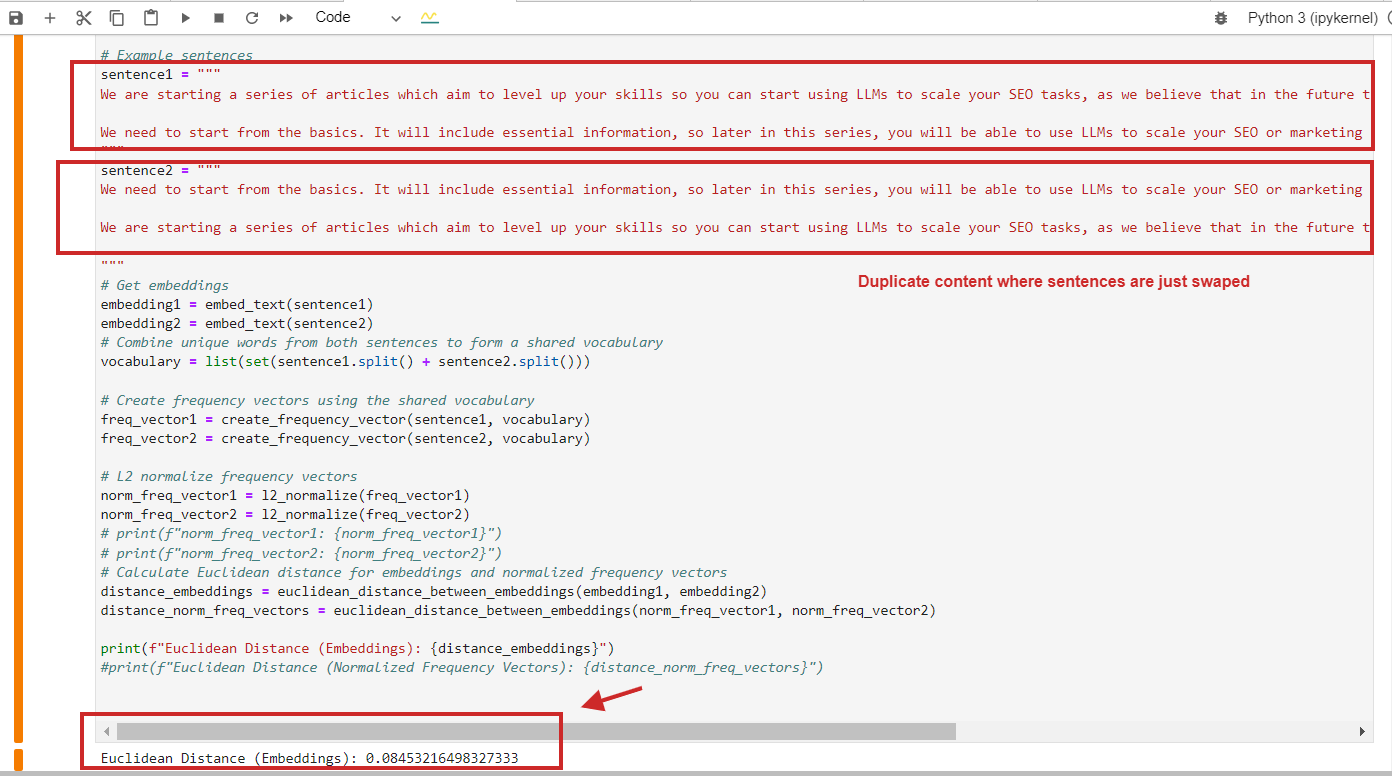 Beispiel für die Berechnung der euklidischen Distanz bei doppeltem Inhalt
Beispiel für die Berechnung der euklidischen Distanz bei doppeltem InhaltNatürlich können Sie die Kosinus-Ähnlichkeit verwenden. Sie erkennt doppelte Inhalte mit einer Kosinus-Ähnlichkeit von 0,9 von 1 (fast identisch).
Hier ist ein wichtiger Punkt, den Sie sich merken sollten: Sie sollten sich nicht nur auf die Kosinus-Ähnlichkeit verlassen, sondern auch andere Methoden verwenden, da die Forschungsarbeit von Netflix nahelegt, dass die Verwendung der Kosinus-Ähnlichkeit zu bedeutungslosen „Ähnlichkeiten“ führen kann.
Wir zeigen, dass die Kosinus-Ähnlichkeit der gelernten Einbettungen tatsächlich beliebige Ergebnisse liefern kann. Wir stellen fest, dass der zugrunde liegende Grund nicht die Kosinus-Ähnlichkeit selbst ist, sondern die Tatsache, dass die gelernten Einbettungen einen Freiheitsgrad haben, der beliebige Kosinus-Ähnlichkeiten erzeugen kann.
Als SEO-Experte müssen Sie nicht in der Lage sein, dieses Dokument vollständig zu verstehen, aber denken Sie daran, dass Untersuchungen zeigen, dass je nach Projektanforderungen und Ergebnis andere Distanzmethoden, wie etwa die euklidische, in Betracht gezogen werden sollten, um falsch-positive Ergebnisse zu reduzieren.
Was ist L2-Normalisierung?
Die L2-Normalisierung ist eine mathematische Transformation, die auf Vektoren angewendet wird, um sie in Einheitsvektoren mit einer Länge von 1 umzuwandeln.
Um es einfach zu erklären: Nehmen wir an, Bob und Alice sind eine lange Strecke gelaufen. Nun wollen wir ihre Richtungen vergleichen. Sind sie ähnlichen Wegen gefolgt oder sind sie in völlig unterschiedliche Richtungen gegangen?
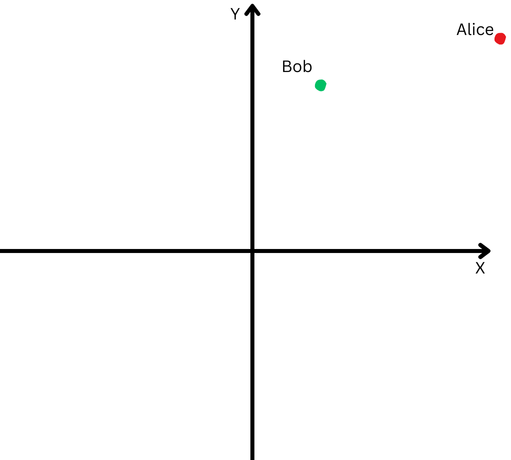 „Alice“ wird durch einen roten Punkt im oberen rechten Quadranten dargestellt und „Bob“ durch einen grünen Punkt.
„Alice“ wird durch einen roten Punkt im oberen rechten Quadranten dargestellt und „Bob“ durch einen grünen Punkt.Da sie jedoch weit von ihrem Ursprungsort entfernt sind, werden wir Schwierigkeiten haben, den Winkel zwischen ihren Pfaden zu messen, weil sie zu weit gegangen sind.
Andererseits können wir nicht behaupten, dass ihre Wege unterschiedlich seien, nur weil sie weit voneinander entfernt sind.
Die L2-Normalisierung entspricht dem Zurückbringen von Alice und Bob in den gleichen geringeren Abstand vom Startpunkt, beispielsweise einen Fuß vom Ursprung, um den Winkel zwischen ihren Pfaden einfacher messen zu können.
Jetzt sehen wir, dass ihre Wegrichtungen trotz ihrer großen Distanz recht ähnlich sind.
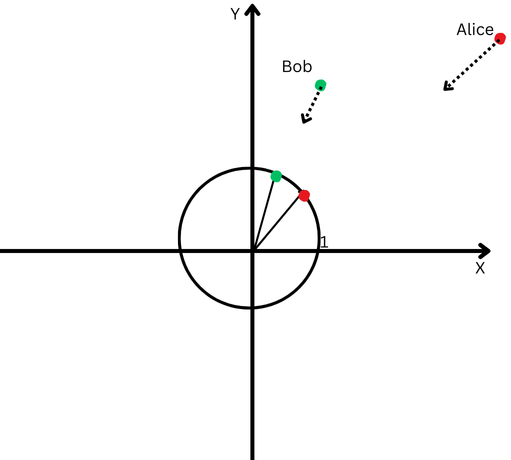 Eine kartesische Ebene mit einem Kreis, dessen Mittelpunkt der Ursprung ist.
Eine kartesische Ebene mit einem Kreis, dessen Mittelpunkt der Ursprung ist.Dies bedeutet, dass wir den Effekt ihrer unterschiedlichen Weglängen (auch als Vektorgrößen bezeichnet) entfernt haben und uns ausschließlich auf die Richtung ihrer Bewegungen konzentrieren können.
Im Kontext von Texteinbettungen hilft uns diese Normalisierung, uns auf die semantische Ähnlichkeit zwischen Texten (die Richtung der Vektoren) zu konzentrieren.
Die meisten Einbettungsmodelle, wie etwa „text-embedding-3-large“ von OpenAI oder „text-embedding-preview-0409“ von Google Vertex AI, geben vornormalisierte Einbettungen zurück, was bedeutet, dass Sie keine Normalisierung vornehmen müssen.
Aber beispielsweise sind die Einbettungen „bert-base-uncased“ des BERT-Modells nicht vornormalisiert.
Abschluss
Dies war das Einführungskapitel zu unserer Artikelserie, die Sie mit dem Jargon des LLMs vertraut machen soll. Ich hoffe, dass Ihnen die Informationen auch ohne einen Doktortitel in Mathematik zugänglich waren.
Wenn Sie immer noch Probleme haben, sich diese zu merken, machen Sie sich keine Sorgen. In den nächsten Abschnitten werden wir auf die hier definierten Definitionen zurückgreifen, und Sie werden sie durch Übung verstehen können.
Die nächsten Kapitel werden noch interessanter:
- Einführung in die Texteinbettungen von OpenAI mit Beispielen.
- Einführung in Goo gle’s Vertex AI-Texteinbettungen mit Beispielen.
- Einführung in Vektordatenbanken.
- So verwenden Sie LLM-Einbettungen für interne Verlinkungen.
- So verwenden Sie LLM-Einbettungen zur Implementierung von Weiterleitungen im großen Maßstab.
- Alles zusammenfügen: LLMs-basiertes WordPress-Plugin für interne Verlinkung.
Das Ziel besteht darin, Ihre Fähigkeiten zu verbessern und Sie auf die Herausforderungen im Bereich SEO vorzubereiten.
Viele von Ihnen werden sagen, dass es käufliche Tools gibt, die solche Dinge automatisch erledigen. Allerdings sind diese Tools nicht in der Lage, viele spezifische Aufgaben entsprechend den Anforderungen Ihres Projekts auszuführen, und erfordern dafür einen individuellen Ansatz.
Die Verwendung von SEO-Tools ist immer gut, aber über entsprechende Kenntnisse zu verfügen ist noch besser!
Mehr Ressourcen:
- Technisches SEO: Die 20-Minuten-Arbeitswochen-Checkliste
- 20 wichtige technische SEO-Tools für Agenturen
- Das vollständige Arbeitsbuch zum technischen SEO-Audit
Vorgestelltes Bild: Krot_Studio/Shutterstock







